Lesson AI Summary
Probability is a fundamental concept in statistics and mathematics that plays a crucial role in decision making and problem solving. It is defined as the likelihood or chance of an event occurring and is represented by a number between 0 and 1, where 0 represents impossibility and 1 represents certainty (Triola, 2018). In this essay, we will discuss the importance of probability, its applications, and how it is calculated.
Firstly, probability is important because it allows us to make informed decisions and predictions based on available information. In everyday life, we are faced with situations where we need to assess the likelihood of an event occurring, such as the probability of rain on a particular day or the chances of winning a game of chance. By understanding probability, we can make better choices and minimize risks (Triola, 2018). In addition, businesses and industries use probability to analyze data and make strategic decisions, leading to increased efficiency and profitability.
Secondly, probability has numerous applications in various fields, including science, economics, and social sciences. In science, probability is used to model and predict outcomes of experiments and research studies. In economics, it is used to analyze financial data and make investment decisions. In social sciences, probability is used to understand human behavior and make predictions about social phenomena (Ross, 2017). These are just a few examples of how probability is used in different areas, highlighting its importance and versatility.
The calculation of probability involves determining the ratio of the number of favorable outcomes to the total number of possible outcomes. For instance, if we want to calculate the probability of rolling a 4 on a standard die, the number of favorable outcomes is 1 (since there is only one side with a 4) and the total number of possible outcomes is 6 (since there are 6 sides on a die). Therefore, the probability of rolling a 4 is 1/6 or 0.167 (Triola, 2018). This simple example demonstrates the basic principle of probability and how it is calculated.
Finally, it is important to note that probability is not always a precise science, and there is always a level of uncertainty involved. This is because probability is based on assumptions and is only an estimate of the likelihood of an event occurring. As such, it is crucial to understand the limitations and potential errors associated with probability calculations (Ross, 2017). Moreover, the interpretation of probability can vary depending on the context and the individual's perception of risk.
In conclusion, probability is a crucial concept with numerous applications in various fields. Its importance lies in its ability to help us make informed decisions and predictions, leading to better outcomes. While it is not a precise science, understanding probability and its calculations can greatly benefit individuals and organizations in various aspects of life. As such, it is an essential concept to learn and apply in our everyday lives.
References:
Ross, S. M. (2017). Introduction to probability models (11th ed.). Academic Press.
Triola, M. F. (2018). Elementary statistics (13th ed.). Pearson.
Lesson Title: Understanding Probability and Maintenance in Technical Vocational Fields
Grade Level: Technical Vocational Students (9-12)
Lesson Duration: 60 minutes
Learning Objectives:
1. Students will understand the concept of probability and its relevance in technical vocational fields.
2. Students will be able to identify and explain the factors that affect the probability of an event.
3. Students will learn about the importance of maintenance in technical vocational fields and its impact on probability.
4. Students will apply their knowledge of probability and maintenance to solve real-world problems in technical vocational fields.
Materials:
- Whiteboard/ chalkboard
- Markers/ chalk
- Handouts with probability problems
- Visual aids (pictures, graphs, charts) related to technical vocational fields
- Computer and projector (optional)
Introduction (10 minutes):
1. Begin the lesson by asking students if they have ever heard of the term "probability." Allow a few students to share their understanding of probability.
2. Explain to students that probability is the likelihood or chance of an event occurring. Give examples of everyday situations where probability is used, such as weather forecasting, sports, and gambling.
3. Inform students that probability is also important in technical vocational fields and that they will be learning about it in today's lesson.
Direct Instruction (20 minutes):
1. Use visual aids to explain the concept of probability in technical vocational fields. Show pictures of machines and equipment and ask students to identify the probability of them breaking down or malfunctioning.
2. Discuss the factors that affect the probability of equipment failure, such as age, usage, maintenance, and external factors.
3. Use real-life examples to demonstrate how probability is calculated. For instance, if a machine has a 20% chance of breaking down, what is the probability of it not breaking down?
4. Discuss the role of data and statistics in determining probability in technical vocational fields.
Guided Practice (15 minutes):
1. Distribute handouts with probability problems related to technical vocational fields.
2. Guide students through solving the problems, emphasizing the use of data and statistics to calculate probability.
3. Encourage students to work in pairs to solve the problems and clarify any doubts they may have.
Independent Practice (10 minutes):
1. Ask students to think of a technical vocational field they are interested in and come up with a scenario where probability is crucial.
2. Have students share their scenarios with the class and explain how probability can be calculated in those situations.
Closure (5 minutes):
1. Summarize the key points of the lesson, emphasizing the importance of probability in technical vocational fields and how it can be calculated.
2. Discuss the impact of probability on maintenance and how it can help prevent equipment failure.
3. Ask students to reflect on what they have learned and how it can be applied in their future careers.
Assessment:
1. Observe students during guided practice and independent practice to assess their understanding of probability in technical vocational fields.
2. Evaluate students' handouts to check for correct problem-solving and understanding of probability concepts.
3. Ask students to write a short paragraph explaining the importance of probability and maintenance in technical vocational fields as a form of summative assessment.
Extension:
1. Have students research and present on how different industries use probability and maintenance to ensure smooth operations and minimize downtime.
2. Invite a guest speaker from a technical vocational field to talk about the importance of probability and maintenance in their job.
3. Have students design a maintenance schedule for a specific machine or equipment based on probability calculations.
Note: This lesson plan can be modified to fit the specific technical vocational fields of the students. Additional time may be needed for the extension activities.
Course Title: Introduction to Probability
Course Description:
This course provides an introduction to the fundamental concepts and principles of probability. Topics covered include basic probability rules, discrete and continuous probability distributions, measures of central tendency and variability, and probability applications in real-world scenarios. Through lectures, problem-solving exercises, and real-world examples, students will gain a solid foundation in probability theory and its applications.
Course Objectives:
1. Understand the basic principles and rules of probability.
2. Analyze and solve problems using discrete and continuous probability distributions.
3. Calculate measures of central tendency and variability.
4. Apply probability concepts to real-world situations.
5. Develop critical thinking and problem-solving skills through probability analysis.
Course Materials:
1. Textbook: Introduction to Probability by Dimitri P. Bertsekas and John N. Tsitsiklis
2. Lecture notes and handouts
3. Calculator (optional)
4. Access to statistical software (optional)
Grading:
1. Quizzes/Assignments: 30%
2. Midterm Exam: 30%
3. Final Exam: 40%
Course Outline:
Week 1:
- Introduction to probability
- Sample spaces and events
- Basic probability rules
- Combinatorics and permutations
Week 2:
- Conditional probability
- Independent and dependent events
- Bayes' theorem
Week 3:
- Discrete random variables
- Probability distributions
- Binomial and Poisson distributions
Week 4:
- Continuous random variables
- Probability density functions
- Normal distribution
Week 5:
- Measures of central tendency
- Mean, median, and mode
- Measures of variability
Week 6:
- Applications of probability in real-world scenarios
- Risk and uncertainty
- Decision making under uncertainty
Week 7:
- Midterm Exam
Week 8:
- Joint and marginal probability
- Conditional distributions
- Multivariate distributions
Week 9:
- Sampling distributions
- Central limit theorem
- Confidence intervals
Week 10:
- Hypothesis testing
- Type I and Type II errors
- P-values
Week 11:
- Regression and correlation
- Probability applications in finance and economics
Week 12:
- Probability applications in healthcare and medicine
- Probability applications in engineering and technology
Week 13:
- Final Exam
Note: The course outline is subject to change at the discretion of the instructor.
Course Policies:
1. Attendance and active participation are expected in all class sessions.
2. Late submissions of assignments will not be accepted.
3. Academic integrity is expected and any form of plagiarism will result in severe consequences.
4. Students are responsible for keeping up with class materials and assignments, even in case of absences.
5. Any special accommodations needed must be discussed with the instructor in advance.
References:
1. Bertsekas, D. P., & Tsitsiklis, J. N. (2008). Introduction to probability. Athena Scientific.
2. Ross, S. M. (2014). A first course in probability. Pearson.
3. Wackerly, D. D., Mendenhall, W., & Scheaffer, R. L. (2014). Mathematical statistics with applications. Cengage Learning.
Disclaimer:
This syllabus is intended to provide an overview of the course and may be subject to change. Any changes will be communicated to students in a timely manner.
Upon completion of this course, students will be able to:
1. Understand the basic concepts of probability and its applications in technical vocational fields.
2. Identify and classify different types of probabilities, such as independent, dependent, and conditional probabilities.
3. Calculate and interpret probabilities using different techniques, including counting methods, tree diagrams, and the laws of probability.
4. Apply the concept of probability to real-world scenarios in technical vocational fields, such as manufacturing, engineering, and data analysis.
5. Analyze and interpret data using probability distributions, such as the binomial and normal distributions.
6. Use tools and technology, such as statistical software, to analyze and solve probability problems in technical vocational fields.
7. Communicate effectively using appropriate mathematical language and notation to explain and justify probability concepts and solutions.
8. Collaborate with peers to solve complex probability problems and present findings through group projects.
9. Demonstrate critical thinking skills by evaluating and interpreting the validity and reliability of data and results obtained from probability experiments.
10. Apply ethical and professional standards when using probability in technical vocational fields, including maintaining confidentiality and acknowledging sources of data.
1) What is the definition of probability?
a) The certainty of an event occurring
b) The likelihood of an event occurring
c) The number of possible outcomes
d) The average of all possible outcomes
Answer: b) The likelihood of an event occurring
2) Which of the following is NOT a valid probability value?
a) -0.5
b) 1
c) 0.25
d) 0
Answer: a) -0.5
3) A fair coin is tossed three times. What is the probability of getting three heads in a row?
a) 1/2
b) 1/3
c) 1/8
d) 1/6
Answer: c) 1/8
4) A deck of cards contains 52 cards, with 13 cards in each suit (hearts, diamonds, clubs, spades). What is the probability of drawing a red card?
a) 1/2
b) 1/4
c) 1/3
d) 1/13
Answer: b) 1/4
5) A bag contains 5 red marbles, 3 blue marbles, and 2 green marbles. If one marble is randomly chosen, what is the probability of choosing a red marble?
a) 1/5
b) 1/4
c) 1/2
d) 2/5
Answer: d) 2/5
AI Conversation
Probability Theory

One fun fact about probability theory is that it can be used to calculate the odds of winning the lottery.
https://www.youtube.com/watch?v=OyddY7DlV58
sample space

https://www.youtube.com/watch?v=0T-CaQCiSf4
Sample space in probability theory refers to the set of all possible outcomes of an experiment. It is a fundamental concept used to analyze and calculate probabilities. Understanding the sample space helps in determining the likelihood of specific events occurring and making informed decisions based on probability.
random variable

https://www.youtube.com/watch?v=3v9w79NhsfI
A random variable in probability theory represents an uncertain outcome of an event. It assigns numerical values to possible outcomes, allowing us to analyze and predict probabilities. It serves as a key tool for understanding and quantifying uncertainty in various fields, including statistics and decision-making.

Probability is a fundamental concept in probability theory. It quantifies the likelihood of an event occurring, ranging from 0 (impossible) to 1 (certain). It helps analyze and predict outcomes in various fields, such as statistics, gambling, and decision-making, by using mathematical models and calculations.
https://www.youtube.com/watch?v=SkidyDQuupA
event

An event in probability theory refers to an outcome or set of outcomes of an experiment. It represents a specific occurrence that can be measured and analyzed. Events are fundamental in calculating probabilities and understanding the likelihood of certain outcomes in various situations.
https://www.youtube.com/watch?v=0T-CaQCiSf4
probability distribution

Probability distribution is a fundamental concept in probability theory. It describes the likelihood of different outcomes occurring in a random experiment. It provides a mathematical framework to analyze and predict the probabilities of events, helping to understand the behavior of random variables and make informed decisions.
https://www.youtube.com/watch?v=cqK3uRoPtk0
law of large numbers

The law of large numbers in probability theory states that as the number of trials or observations increases, the average or expected value of the outcomes will converge to the true probability or expected value.
https://www.youtube.com/watch?v=VpuN8vCQ--M
conditional probability

Conditional probability is a concept in probability theory that measures the likelihood of an event occurring given that another event has already occurred. It helps us understand the relationship between events and allows us to make more accurate predictions based on additional information.
https://www.youtube.com/watch?v=6xPkG2pA-TU
independence

Independence in probability theory refers to events that do not influence each other's occurrence. It allows for the calculation of joint probabilities by multiplying the individual probabilities. Independence is crucial in various statistical analyses and helps simplify complex probability problems.
https://www.youtube.com/watch?v=pIfpHdGVwLU
Random variable

One fun fact about the random variable in hard skills is that it can be used to model the probability distribution of outcomes in various fields such as mathematics, computer science, and engineering, providing a mathematical framework to analyze and predict the likelihood of different events occurring.
https://www.youtube.com/watch?v=3v9w79NhsfI
expected value

https://www.youtube.com/watch?v=qafPcWNUiM8
Expected value is a measure of the average outcome of a random variable. It represents the long-term average of a variable's possible values, weighted by their probabilities. It helps in understanding the central tendency of a random variable and is useful in decision-making and risk assessment.
standard deviation
/calculate-a-sample-standard-deviation-3126345-v4-CS-01-5b76f58f46e0fb0050bb4ab2.png)
Standard deviation is a measure of the dispersion or variability of a random variable's values. It quantifies how much the values deviate from the mean. A higher standard deviation indicates greater variability, while a lower standard deviation suggests less variability in the data.
https://www.youtube.com/watch?v=2egl_5c8i-g
probability distribution

https://www.youtube.com/watch?v=cqK3uRoPtk0
Probability distribution refers to the likelihood of different outcomes occurring in a random variable. It provides a summary of all possible values and their associated probabilities. This distribution helps in understanding the likelihood of specific events and aids in making predictions or analyzing data in various fields like statistics, finance, and science.
cumulative distribution function

The cumulative distribution function (CDF) is a function that gives the probability that a random variable takes on a value less than or equal to a given value. It provides a way to understand the probability distribution of a random variable and is useful in statistical analysis.
https://www.youtube.com/watch?v=3xAIWiTJCvE
probability mass function

A probability mass function (PMF) is a function that describes the probability distribution of a discrete random variable. It assigns probabilities to each possible outcome of the random variable, allowing us to analyze the likelihood of different events occurring.
https://www.youtube.com/watch?v=zW1_iugJvF0
probability density function

A probability density function (PDF) describes the likelihood of a random variable taking on different values. It provides a continuous distribution by assigning probabilities to intervals rather than specific values. The PDF helps analyze and understand the behavior of random variables in various statistical and mathematical applications.
https://www.youtube.com/watch?v=Fvi9A_tEmXQ
independence

Independence in the context of random variables refers to the absence of any relationship or influence between two or more variables. It means that the occurrence or value of one variable does not affect or provide any information about the occurrence or value of another variable.
https://www.youtube.com/watch?v=F6H50Hbulbk
variance

Variance measures the spread or variability of a random variable's values around its mean. It quantifies how much the values deviate from the average, providing insight into the distribution's dispersion.
https://www.youtube.com/watch?v=2egl_5c8i-g
Probability

One fun fact about probability in hard skills is that the concept of probability was first introduced in the 17th century by French mathematicians Blaise Pascal and Pierre de Fermat while they were discussing a gambling problem.
https://www.youtube.com/watch?v=ZF04LVXB5C8
sample space

Sample space refers to the set of all possible outcomes in a probability experiment. It is a fundamental concept in probability theory and helps determine the likelihood of events occurring. Understanding the sample space is crucial for calculating probabilities accurately.
https://www.youtube.com/watch?v=SkidyDQuupA
event
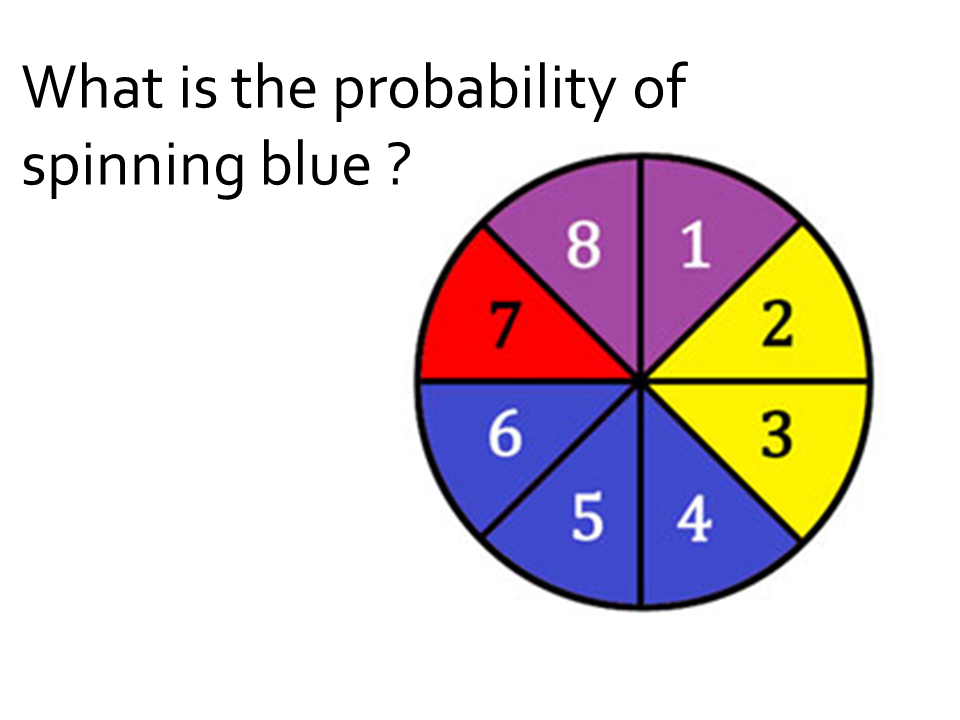
An event in the context of probability refers to a specific outcome or result that can occur in an experiment or situation. It represents the possible outcomes that can be observed and analyzed using mathematical principles to determine the likelihood or probability of its occurrence.
https://www.youtube.com/watch?v=0T-CaQCiSf4
complement

In probability, the complement refers to the event that does not occur. It is the opposite outcome of a given event. Complement is used to calculate the probability of an event by subtracting its probability from 1.
https://www.youtube.com/watch?v=0T-CaQCiSf4
union

Union in probability refers to the event that at least one of two or more events will occur. It is represented by the symbol "∪" and is calculated by adding the probabilities of the individual events, while subtracting the probability of their intersection.
https://www.youtube.com/watch?v=vqKAbhCqSTc
conditional probability

Conditional probability is a measure of the likelihood of an event occurring given that another event has already occurred. It helps in understanding the relationship between events and is calculated by dividing the probability of the intersection of two events by the probability of the given event.
https://www.youtube.com/watch?v=6xPkG2pA-TU
probability function

A probability function is a mathematical tool used in probability theory to assign probabilities to different outcomes of an event. It maps each possible outcome to a probability value, enabling the calculation of the likelihood of events occurring.
https://www.youtube.com/watch?v=i6_byEFjKEA
intersection

Intersection in the context of probability refers to the event where two or more events occur simultaneously. It is represented by the intersection symbol (∩) and is used to calculate the probability of both events happening together.
https://www.youtube.com/watch?v=B1v9OeCTlu0
probability axioms

Probability axioms are fundamental principles that govern the behavior of probabilities. They include the axiom of non-negativity, which states that probabilities cannot be negative, and the axiom of total probability, which states that the sum of probabilities of all possible outcomes is equal to 1.
https://www.youtube.com/watch?v=pA83XtLeVig