Lesson AI Summary
"Quantum Gates and Circuits" is an immersive augmented and virtual reality experience designed to introduce users to the foundational concepts of quantum computing. Participants will explore the essential operations of quantum gates, such as the Hadamard and NOT gates, and learn how these gates manipulate qubits—units of quantum information that can exist in multiple states simultaneously. The experience highlights the significance of superposition, allowing users to understand how qubits can represent both 0 and 1 at the same time, leading to enhanced computational power.
Through interactive simulations, users will witness how quantum gates create complex circuits that enable quantum parallelism and entanglement, which are crucial for advanced quantum algorithms. Participants will also engage with the concept of measurement, observing how qubit states collapse to yield definite outcomes. By the end of this experience, users will gain a comprehensive understanding of quantum circuits, the role of quantum gates, and the transformative potential of quantum computing in solving problems beyond the reach of classical systems.
### Quantum Gates and Circuits
Quantum computing represents a transformative paradigm in the field of computation, leveraging the principles of quantum mechanics to process information. Central to this technology are quantum gates and circuits, which serve analogous functions to classical logic gates and circuits but operate on quantum bits, or qubits. This essay will explore the fundamentals of quantum gates, their role in quantum circuits, and the implications of these components in advancing quantum computation.
Quantum gates are the building blocks of quantum circuits, manipulating qubits through operations that are fundamentally different from classical bits. Unlike classical bits, which can be either 0 or 1, qubits can exist in a superposition of states, allowing them to represent both values simultaneously (Nielsen & Chuang, 2010). Quantum gates perform unitary operations on qubits, transforming their state while preserving the overall probability amplitude. Common examples of quantum gates include the Pauli-X, Hadamard, and CNOT gates, each serving specific functions in quantum computation (Nielsen & Chuang, 2010). For instance, the Hadamard gate creates superposition, while the CNOT gate entangles two qubits, crucial for many quantum algorithms (Shor, 1997).
Quantum circuits comprise interconnected quantum gates arranged in a specific sequence to perform complex computations. A quantum circuit is typically represented as a series of qubits and gates, similar to classical circuits but with the added complexity of quantum behavior. The arrangement and choice of gates within a quantum circuit determine the algorithm's functionality and efficiency (Kjaergaard et al., 2020). Unlike classical circuits, where the operations are deterministic, quantum circuits yield probabilistic outcomes, necessitating multiple runs to obtain reliable results. This feature underpins the strength of quantum algorithms, enabling them to solve certain problems exponentially faster than classical counterparts.
The implications of quantum gates and circuits extend beyond theoretical computation; they hold the potential to revolutionize various fields, including cryptography, optimization, and drug discovery. For instance, Shor's algorithm demonstrates how quantum circuits can factor large numbers efficiently, posing a significant challenge to classical encryption methods (Shor, 1997). Similarly, quantum circuits designed for optimization problems can explore multiple solutions concurrently, offering unprecedented speed compared to traditional algorithms (Farhi et al., 2014). As research progresses, the practical realization of quantum gates and circuits will pave the way for breakthroughs in technology and computation.
In conclusion, quantum gates and circuits form the foundation of quantum computing, enabling the manipulation and processing of information in ways classical systems cannot achieve. Their unique properties, such as superposition and entanglement, allow for the development of algorithms that can outperform classical counterparts, showcasing the transformative potential of quantum computation. As advancements in this field continue, the effective design and implementation of quantum gates and circuits will be crucial in unlocking new computational capabilities and applications.
### References
Farhi, E., Goldstone, J., & Gutmann, S. (2014). A quantum approximate optimization algorithm. *arXiv preprint arXiv:1404.3729*.
Kjaergaard, M., Schwartz, M. D., Braumüller, J., & Gambetta, J. M. (2020). Superconducting Qubits: Current State of Play. *Annual Review of Condensed Matter Physics*, 11(1), 369-395. https://doi.org/10.1146/annurev-conmatphys-031119-050605
Nielsen, M. A., & Chuang, I. L. (2010). *Quantum Computation and Quantum Information* (10th Anniversary ed.). Cambridge University Press.
Shor, P. W. (1997). Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. *SIAM Journal on Computing*, 26(5), 1484-1509. https://doi.org/10.1137/S0097539795293172
### Lesson Plan: Introduction to Quantum Gates and Circuits
**Grade Level:** Technical Vocational Students
**Duration:** 2 hours
**Subject:** Quantum Computing
**Instructor:** [Instructor's Name]
**Location:** [Classroom/Lab Name]
---
#### **Objectives:**
By the end of this lesson, students will be able to:
1. Understand the basic concepts of quantum gates and circuits.
2. Identify and describe the function of different quantum gates.
3. Explain how quantum circuits are constructed and how they operate.
4. Discuss the maintenance and troubleshooting of quantum circuits.
---
#### **Materials Needed:**
- Whiteboard and markers
- Projector and computer for presentations
- Quantum computing simulation software (e.g., IBM Quantum Experience, Qiskit)
- Handouts with diagrams of quantum gates and circuits
- Sample problems for group activities
- Access to online resources or textbooks on quantum computing
---
#### **Lesson Outline:**
**1. Introduction to Quantum Computing (15 minutes)**
- Discuss the evolution of computing: classical vs. quantum.
- Introduce the basic principles of quantum mechanics relevant to computing (superposition, entanglement).
- Explain why quantum computing is significant and its potential applications.
**2. Overview of Quantum Gates (20 minutes)**
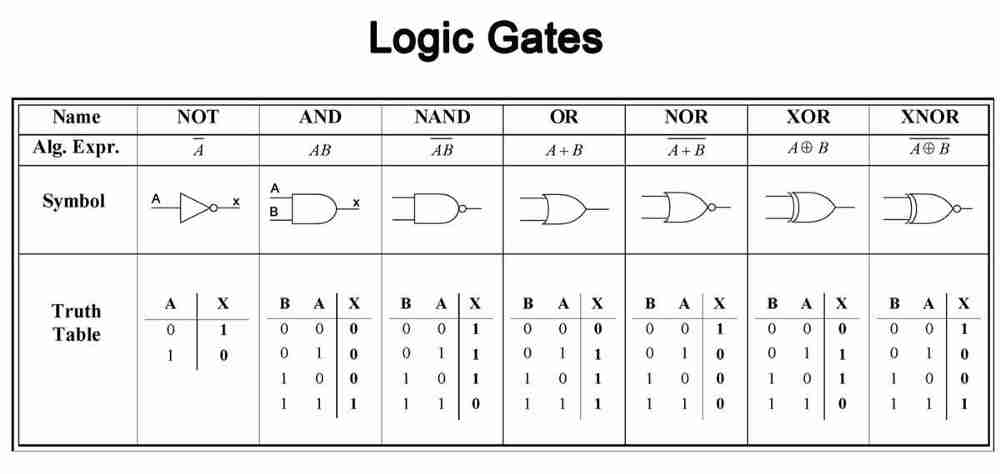
- Define what quantum gates are and how they differ from classical logic gates.
- Describe basic quantum gates:
- **Hadamard Gate (H)**
- **Pauli-X Gate (NOT)**
- **Pauli-Y Gate**
- **Pauli-Z Gate**
- **CNOT Gate (Controlled NOT)**
- Use visual aids to illustrate the function of each gate.
- Discuss the concept of qubits and how gates manipulate qubits.
**3. Quantum Circuits (20 minutes)**
- Define quantum circuits and their importance in quantum computing.
- Explain how quantum gates are arranged to form quantum circuits.
- Walk through simple examples of quantum circuits using the gates discussed.
- Show how to represent quantum circuits using diagrams.
**4. Hands-On Activity: Building Quantum Circuits (30 minutes)**
- Divide students into small groups.
- Provide access to quantum computing simulation software.
- Assign each group a simple task to create a quantum circuit using specific gates (e.g., create a circuit that puts a qubit in superposition).
- Encourage students to test their circuits and observe the outcomes.
- Each group will present their circuit and findings to the class.
**5. Maintenance and Troubleshooting of Quantum Circuits (20 minutes)**
- Discuss common issues that can arise in quantum circuits (decoherence, noise).
- Explain maintenance practices for quantum hardware and software.
- Share best practices for troubleshooting quantum circuits.
- Discuss the importance of error correction in quantum computing.
**6. Q&A and Discussion (15 minutes)**
- Open the floor for questions.
- Encourage students to discuss what they found interesting or challenging.
- Provide additional resources for students interested in exploring quantum computing further.
---
#### **Assessment:**
- Participation in group activities and discussions.
- A short quiz at the end of the lesson covering key concepts (e.g., definitions, functions of quantum gates, understanding circuit designs).
- Optional: Written reflection on what they learned about quantum gates and circuits.
---
#### **Extensions:**
- Assign a research project on a specific aspect of quantum computing (e.g., advancements in quantum algorithms).
- Organize a guest lecture with a quantum computing professional.
- Create a lab session focused on advanced quantum circuits and algorithms.
---
#### **Conclusion:**
This lesson plan aims to provide technical vocational students with a foundational understanding of quantum gates and circuits. By combining theoretical knowledge with hands-on activities, students will gain practical experience that can be applied in the field of quantum computing.
# Syllabus for Quantum Gates and Circuits
## Course Title: Quantum Gates and Circuits
### Course Description
This course provides an introduction to quantum computing, focusing on quantum gates and circuits. Students will learn the fundamental principles of quantum mechanics that underpin quantum computation, explore the operation and implementation of quantum gates, and gain practical experience in designing quantum circuits. By the end of the course, students will be equipped with the necessary skills to understand and construct basic quantum algorithms.
### Course Objectives
By the end of this course, students will be able to:
1. Understand the principles of quantum mechanics relevant to quantum computing.
2. Describe the function and role of quantum gates in quantum circuits.
3. Analyze and construct quantum circuits using basic quantum gates.
4. Implement quantum algorithms using simulation tools.
5. Evaluate the potential and limitations of quantum computing.
### Prerequisites
- Basic understanding of linear algebra and probability theory.
- Familiarity with classical computing concepts.
### Course Format
- Lectures: 2 sessions per week (1.5 hours each)
- Labs: 1 session per week (2 hours)
- Assignments: Weekly readings and problem sets
- Final Project: Design and implementation of a quantum circuit
### Required Texts
- "Quantum Computation and Quantum Information" by Michael A. Nielsen and Isaac L. Chuang
- Supplemental readings from peer-reviewed journals and online resources will be provided throughout the course.
### Schedule
#### Week 1: Introduction to Quantum Computing
- Overview of quantum computing
- Classical vs. quantum information
- Quantum bits (qubits)
#### Week 2: Fundamentals of Quantum Mechanics
- Superposition and entanglement
- Quantum states and the Bloch sphere
#### Week 3: Quantum Gates
- Introduction to quantum gates
- Single-qubit gates (Pauli-X, Pauli-Y, Pauli-Z, Hadamard)
- Multi-qubit gates (CNOT, Toffoli)
#### Week 4: Quantum Circuits
- Overview of quantum circuits
- Circuit representation and notation
- Basic circuit design principles
#### Week 5: Measurement in Quantum Computing
- Quantum measurement
- Collapse of the wave function
- Measurement-based quantum computation
#### Week 6: Quantum Algorithms: Part 1
- Introduction to quantum algorithms
- Deutsch-Josza algorithm
- Grover's search algorithm
#### Week 7: Quantum Algorithms: Part 2
- Shor's algorithm for integer factorization
- Quantum Fourier transform
#### Week 8: Quantum Circuit Simulation
- Introduction to quantum simulation tools (e.g., Qiskit, Cirq)
- Hands-on lab: Building and simulating basic circuits
#### Week 9: Error Correction in Quantum Computing
- Quantum noise and decoherence
- Overview of quantum error correction codes
- Practical implications for quantum circuits
#### Week 10: Advanced Quantum Gates and Circuits
- Implementing advanced gates (swap, controlled-U)
- Quantum circuit optimization techniques
#### Week 11: Real-World Applications of Quantum Computing
- Quantum computing in cryptography, optimization, and material science
- Case studies of quantum algorithms in practice
#### Week 12: Final Project Preparation
- Project proposal presentations
- Peer feedback and refinement
#### Week 13: Final Project Presentations
- Student presentations of final projects
- Class discussion and critique
### Assessment and Grading
- Weekly Assignments: 30%
- Lab Participation: 20%
- Midterm Exam: 20%
- Final Project: 30%
### Academic Integrity
Students are expected to adhere to the highest standards of academic integrity. Cheating, plagiarism, or any form of academic dishonesty will not be tolerated and will result in disciplinary action.
### Office Hours
Instructor: [Instructor Name]
Office Hours: [Days and Times]
Email: [Instructor Email]
---
This syllabus is designed to provide a comprehensive overview of quantum gates and circuits, ensuring that students gain both theoretical knowledge and practical skills in quantum computing.
### Learning Objectives for Quantum Gates and Circuits Course
1. **Understand Quantum Fundamentals**
- Describe the basic principles of quantum mechanics, including superposition and entanglement, and explain their significance in quantum computing.
2. **Identify Quantum Gates**
- Recognize and define the primary quantum gates (e.g., Hadamard, Pauli-X, CNOT, Toffoli) and their functions in quantum circuits.
3. **Analyze Quantum Circuits**
- Construct and analyze simple quantum circuits using various quantum gates, understanding how each gate manipulates qubit states.
4. **Implement Quantum Algorithms**
- Demonstrate the ability to implement basic quantum algorithms (e.g., Deutsch-Josza, Grover’s algorithm) using quantum gates and circuits.
5. **Utilize Quantum Simulation Tools**
- Use quantum computing simulation software to design, visualize, and test quantum circuits, gaining hands-on experience with quantum programming environments.
6. **Evaluate Quantum Circuit Efficiency**
- Assess the efficiency of quantum circuits in terms of gate count and circuit depth, and compare the performance of quantum circuits against classical counterparts.
7. **Explore Quantum Error Correction**
- Explain the principles of quantum error correction and its importance in building reliable quantum systems.
8. **Apply Quantum Concepts to Real-World Problems**
- Investigate and present how quantum gates and circuits can be applied to solve real-world problems in fields such as cryptography, optimization, and complex simulations.
9. **Collaborate on Group Projects**
- Work effectively in teams to design and present a comprehensive quantum circuit project, demonstrating collaboration and problem-solving skills.
10. **Communicate Quantum Concepts**
- Clearly articulate the concepts of quantum gates and circuits through written reports and oral presentations, making complex ideas accessible to a broader audience.
By the end of this course, students will have a foundational understanding of quantum gates and circuits, equipping them with skills applicable in the evolving field of quantum computing.
Certainly! Here are five multiple-choice questions about Quantum Gates and Circuits:
### Question 1:
What is the primary function of a quantum gate in quantum computing?
A) To perform classical logic operations
B) To manipulate qubits
C) To store data
D) To measure qubit states
**Answer:** B) To manipulate qubits
---
### Question 2:
Which of the following quantum gates is known for flipping the state of a qubit from |0⟩ to |1⟩ and vice versa?
A) Hadamard Gate
B) CNOT Gate
C) Pauli-X Gate
D) T Gate
**Answer:** C) Pauli-X Gate
---
### Question 3:
In a quantum circuit, what does a CNOT gate do when applied to two qubits?
A) It flips the first qubit
B) It flips the second qubit if the first qubit is |1⟩
C) It entangles the qubits
D) It measures the state of both qubits
**Answer:** B) It flips the second qubit if the first qubit is |1⟩
---
### Question 4:
What is the effect of a Hadamard gate on a qubit in the state |0⟩?
A) It leaves the qubit unchanged
B) It transforms it to |1⟩
C) It transforms it to a superposition state (|0⟩ + |1⟩)/√2
D) It measures the qubit
**Answer:** C) It transforms it to a superposition state (|0⟩ + |1⟩)/√2
---
### Question 5:
Which of the following statements is true about quantum circuits?
A) Quantum circuits can only implement classical algorithms.
B) Quantum circuits can create and manipulate entangled states.
C) Quantum circuits are less efficient than classical circuits for all problems.
D) Quantum circuits do not involve qubits.
**Answer:** B) Quantum circuits can create and manipulate entangled states.
---
Feel free to use or modify these questions as needed!
AI Conversation
Hadamard Gate
The Hadamard gate transforms a qubit from a definite state into a superposition, creating equal probabilities of measuring |0⟩ or |1⟩. It is crucial for initiating quantum parallelism and is widely used in quantum algorithms to exploit the unique properties of quantum computation.

not (x) gate
The NOT gate, also known as the X gate, flips the state of a qubit: |0⟩ becomes |1⟩ and vice versa. It is a fundamental single-qubit gate, analogous to the classical NOT operation, and is essential for constructing more complex quantum logic circuits.
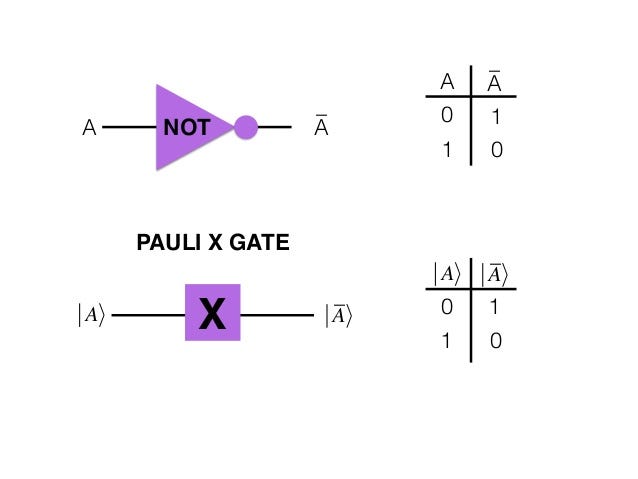
quantum gates
Quantum gates are operations that change the state of qubits. Examples include the NOT (X) gate, which flips a qubit’s state, and the Hadamard gate, which creates superpositions. Gates are represented mathematically and are the building blocks for constructing quantum circuits.
https://www.youtube.com/watch?v=QXJ96Kyt6TA
qubit
A qubit is the basic unit of quantum information, analogous to a classical bit but capable of existing in a superposition of states. Its quantum nature allows it to represent both 0 and 1 simultaneously, enabling powerful computational possibilities not achievable with classical bits.
https://www.youtube.com/watch?v=30U2DTfIrOU
quantum gates and circuits
Quantum gates and circuits are the fundamental building blocks of quantum computing. They manipulate qubits using precise operations, enabling superposition, entanglement, and complex computations. Understanding their structure and function is essential for harnessing the unique capabilities of quantum information processing and developing advanced quantum algorithms.
https://www.youtube.com/watch?v=nGPr1QM_XrY
entanglement
Entanglement is a uniquely quantum phenomenon where two or more qubits become correlated so that the state of one instantly affects the other, regardless of distance. Entanglement enables powerful quantum protocols and is essential for many quantum algorithms and communication schemes.

measurement
Measurement is the process of observing a qubit’s state, collapsing its superposition into a definite outcome—either |0⟩ or |1⟩. Measurement is probabilistic, with outcomes determined by the qubit’s quantum state prior to measurement. It is the final step in extracting results from quantum circuits.

superposition
Superposition is a fundamental quantum property where a qubit exists in a combination of the |0⟩ and |1⟩ states. This allows quantum computers to process multiple possibilities at once, greatly increasing computational parallelism and efficiency compared to classical systems.
https://www.youtube.com/watch?v=nzt4csepgnY
quantum circuit
A quantum circuit is a sequence of quantum gates applied to one or more qubits. The arrangement and order of gates determine the computation performed. Circuits are often visualized as diagrams, making it easier to design and analyze quantum algorithms.
https://www.youtube.com/watch?v=3OyXA0QgnYI