AI Conversation
Historia y evolución del concepto de Integral ( Newron, Leibniz, Riemann, Lebesgue)

Isaac Newton y Gottfried Wilhelm Leibniz desarrollaron el cálculo integral de forma independiente en el siglo XVII, pero sus notaciones eran diferentes. La notación de Leibniz es la que más se utiliza hoy en día.
https://www.youtube.com/watch?v=nHcmJUMVv8I
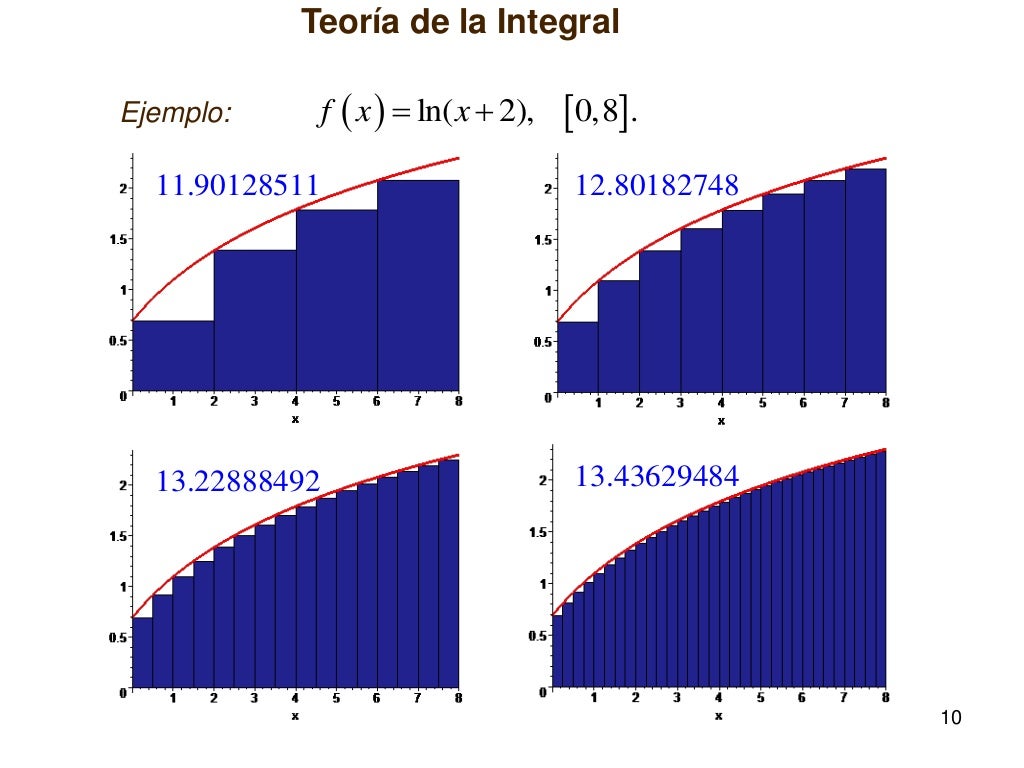
Riemann revolucionó el concepto de integral al introducir la integral de Riemann en el siglo XIX, extendiendo las ideas de Newton y Leibniz. Su enfoque se centró en la suma de áreas bajo curvas mediante particiones, sentando las bases para la integral de Lebesgue, que permitió integrar funciones más generales.
newton

Isaac Newton, junto con Leibniz, desarrolló el cálculo diferencial e integral en el siglo XVII. Su enfoque se centró en el cálculo de áreas bajo curvas y el cambio continuo. Este trabajo sentó las bases para las integrales de Riemann y Lebesgue, que refinaron y ampliaron el concepto en siglos posteriores.
cálculo infinitesimal
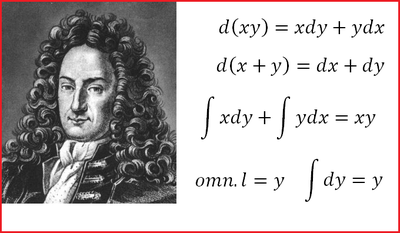
El cálculo infinitesimal, desarrollado por Newton y Leibniz, revolucionó el concepto de integral al introducir el cálculo diferencial e integral. Riemann refinó la integral con su enfoque basado en sumas, mientras que Lebesgue amplió el concepto permitiendo integrar funciones más generales, transformando profundamente el análisis matemático.
función

La función es clave en la evolución del concepto de integral. Newton y Leibniz desarrollaron el cálculo diferencial e integral. Riemann introdujo la integral definida mediante sumas, mientras que Lebesgue refinó el concepto, permitiendo integrar funciones más generales, ampliando así el alcance y aplicación del cálculo integral.

Henri Lebesgue revolucionó el cálculo integral al introducir la integral de Lebesgue a principios del siglo XX. A diferencia de las integrales de Newton y Leibniz, y la de Riemann, su enfoque permitió integrar funciones más generales, ampliando significativamente el ámbito de aplicación del análisis matemático.
Gottfried Wilhelm Leibniz, junto con Newton, desarrolló el cálculo diferencial e integral en el siglo XVII. Introdujo la notación moderna para la integral, ∫, y su enfoque se centró en la suma de infinitesimales. Su trabajo sentó las bases para el desarrollo posterior por Riemann y Lebesgue.
notación
La notación de la integral ha evolucionado desde Newton y Leibniz, quienes introdujeron conceptos fundamentales. Leibniz usó el símbolo ∫ para representar sumas infinitesimales. Riemann formalizó la integral mediante particiones, y Lebesgue amplió el concepto con su teoría de medida, permitiendo integrar funciones más generales.
área bajo la curva
El concepto de "área bajo la curva" es fundamental en la evolución del cálculo integral. Newton y Leibniz desarrollaron el cálculo diferencial e integral, estableciendo las bases. Riemann formalizó la integral mediante sumas, mientras que Lebesgue introdujo una integral más general, ampliando su aplicabilidad y precisión en el análisis matemático.
Newton

El newton es la unidad de medida de fuerza en el Sistema Internacional, nombrada en honor a Isaac Newton. Un newton es la fuerza necesaria para acelerar un kilogramo de masa a un metro por segundo al cuadrado.
https://www.youtube.com/watch?v=OK1bCqkn6Vk
cálculo integral

El cálculo integral, en el contexto de Newton, se refiere al desarrollo de técnicas para calcular áreas bajo curvas y acumulación de cantidades. Newton, junto con Leibniz, es cofundador del cálculo, estableciendo el vínculo entre derivadas e integrales, conocido como el teorema fundamental del cálculo.
https://www.youtube.com/watch?v=FHLsTqxW9uc
flujo

https://www.youtube.com/watch?v=YL8DJTGBPwE
En el contexto de Newton, "flujo" se refiere al flujo de un campo vectorial a través de una superficie. Es un concepto clave en el cálculo vectorial y se utiliza para describir cómo un campo, como el campo gravitatorio, interactúa con superficies en el espacio tridimensional.
cálculo diferencial

El cálculo diferencial, desarrollado por Isaac Newton, es una rama fundamental de las matemáticas que estudia cómo cambian las funciones. Newton introdujo el concepto de derivada, permitiendo analizar tasas de cambio instantáneas y resolver problemas de movimiento y dinámica, sentando las bases para el desarrollo de la física clásica.
https://www.youtube.com/watch?v=midvTt2_PfI
antiderivada

La antiderivada, en el contexto de Newton, se refiere al proceso inverso de la derivación, conocido como integración. Newton desarrolló el cálculo diferencial e integral, estableciendo el teorema fundamental del cálculo, que conecta derivadas e integrales, permitiendo calcular áreas bajo curvas y resolver problemas de movimiento.
teorema fundamental

https://www.youtube.com/watch?v=Chy8eCoT9sw
El teorema fundamental del cálculo, en el contexto de Newton, establece la conexión entre derivadas e integrales. Newton desarrolló el cálculo diferencial e integral simultáneamente, mostrando que la derivada de una integral es la función original, unificando así el análisis matemático y facilitando el estudio del movimiento y el cambio.
método de límites
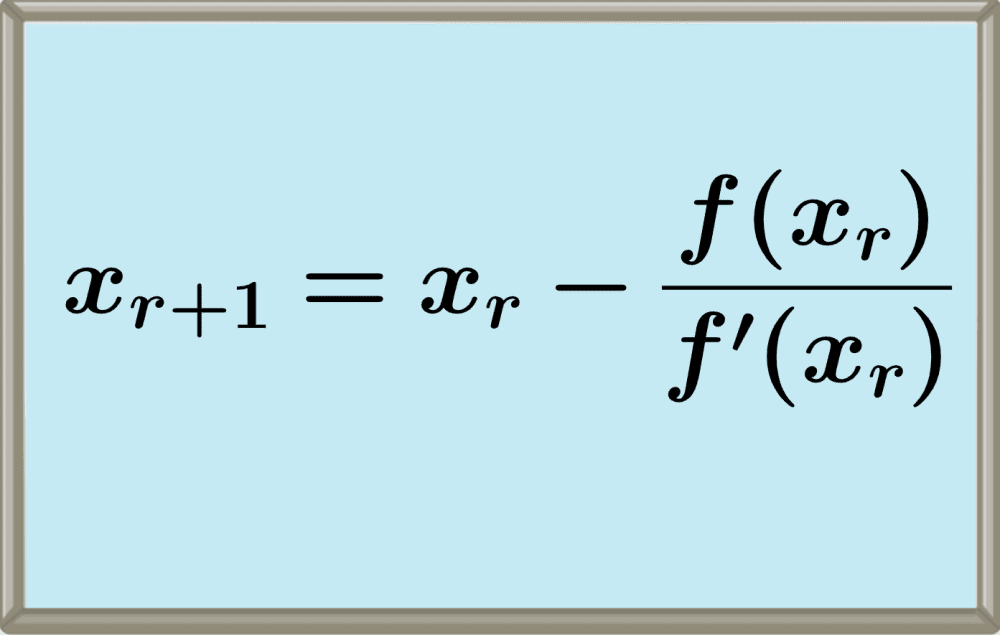
El método de límites, en el contexto de Newton, se refiere a su enfoque para calcular derivadas y tangentes. Newton utilizó límites para describir el cambio infinitesimal en funciones, sentando las bases del cálculo diferencial. Este método permitió el desarrollo de su teoría del movimiento y la gravitación universal.
https://www.youtube.com/watch?v=-5e2cULI3H8
curvas
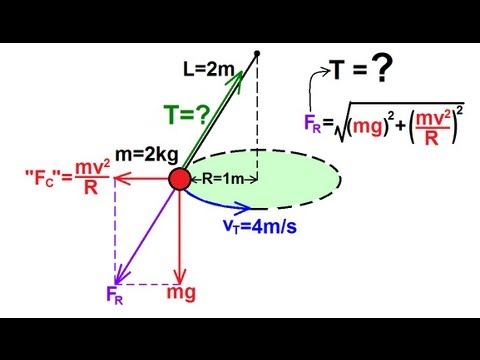
En el contexto de Newton, las curvas se refieren a trayectorias geométricas que describen el movimiento de objetos bajo la influencia de fuerzas. Newton estudió cómo las fuerzas afectan el movimiento, formulando leyes que explican cómo las curvas resultantes, como órbitas planetarias, son determinadas por la gravedad y otras fuerzas.
https://www.youtube.com/watch?v=FMWxvYpGRBI
integración

La integración en el contexto de Newton se refiere al cálculo integral, una rama fundamental del cálculo matemático. Newton, junto con Leibniz, desarrolló el cálculo integral, que permite calcular áreas bajo curvas y resolver problemas de acumulación y cambio, siendo esencial para la física y la ingeniería.
Leibniz

Gottfried Wilhelm Leibniz inventó el cálculo de manera independiente y casi simultánea a Isaac Newton, pero su notación matemática es la que se utiliza principalmente hoy en día.
análisis infinitesimal

El análisis infinitesimal, desarrollado por Leibniz, es una rama del cálculo que estudia cambios infinitesimales y sus aplicaciones. Leibniz introdujo el uso de diferenciales y el símbolo "d" para representar cambios pequeños, estableciendo las bases del cálculo diferencial e integral, fundamentales para el avance de las matemáticas modernas.
https://www.youtube.com/watch?v=ov6kRag2YA0
cálculo

Gottfried Wilhelm Leibniz fue un matemático y filósofo alemán que co-desarrolló el cálculo diferencial e integral de manera independiente a Newton. Su notación, especialmente el uso de "d" para diferenciales, sigue siendo fundamental. Leibniz enfatizó la claridad y la lógica en las matemáticas, influyendo profundamente en el desarrollo posterior del cálculo.
teorema fundamental

El teorema fundamental del cálculo, en el contexto de Leibniz, establece la conexión entre la derivación y la integración. Leibniz, junto con Newton, desarrolló el cálculo diferencial e integral, proporcionando herramientas matemáticas esenciales para resolver problemas de cambio y acumulación en diversas disciplinas científicas.
https://www.youtube.com/watch?v=7jiZyS3pEfc
notación

La notación de Leibniz es fundamental en el cálculo diferencial e integral. Introdujo símbolos como "d" para diferenciales y el signo de integral ∫, facilitando el desarrollo y comprensión del cálculo. Su notación clara y sistemática permitió avances significativos en matemáticas, influyendo en generaciones de matemáticos posteriores.
regla del producto

La "regla del producto" es un principio fundamental del cálculo diferencial, formulado por Leibniz. Establece que la derivada del producto de dos funciones es igual a la derivada de la primera por la segunda más la primera por la derivada de la segunda: (uv)' = u'v + uv'.
https://www.youtube.com/watch?v=HleM9SppgBM
diferencial

En el contexto de Leibniz, el diferencial es un concepto fundamental en el cálculo infinitesimal. Leibniz introdujo la notación "dx" para representar un cambio infinitesimal en la variable x, permitiendo el desarrollo de reglas de derivación y cálculo diferencial, esenciales para el análisis matemático y la comprensión del cambio continuo.
https://www.youtube.com/watch?v=DTlPt5KPnzE
controversia

La controversia en el contexto de Leibniz se centra en su disputa filosófica con Newton sobre el cálculo. Leibniz desarrolló su propia notación, que aún se usa hoy, pero fue acusado de plagio. Este conflicto subraya debates sobre originalidad y propiedad intelectual en la ciencia del siglo XVII.
https://www.youtube.com/watch?v=axZTv5YJssA
contribuciones matemáticas

Gottfried Wilhelm Leibniz, un destacado matemático y filósofo alemán, contribuyó significativamente al desarrollo del cálculo diferencial e integral, independientemente de Newton. Introdujo la notación moderna para el cálculo, facilitando su comprensión y aplicación. Sus ideas sobre el sistema binario también sentaron las bases para la informática moderna.
https://www.youtube.com/watch?v=LBpabZZ_3Iw
Riemann

El matemático Bernhard Riemann, conocido por su hipótesis sobre los ceros de la función zeta, también fue pionero en geometría diferencial, sentando las bases para la teoría de la relatividad de Einstein.
https://www.youtube.com/watch?v=zlm1aajH6gY
partición

En el contexto de Riemann, una partición se refiere a la división de un intervalo en subintervalos más pequeños. Esto es fundamental para definir la integral de Riemann, donde se calcula la suma de áreas bajo una curva aproximando mediante rectángulos, mejorando la precisión al refinar la partición.
https://www.youtube.com/watch?v=x0It_iX9W0o
integrabilidad

La integrabilidad en el contexto de Riemann se refiere a la capacidad de una función para ser integrada usando la integral de Riemann. Una función es integrable en este sentido si su conjunto de discontinuidades tiene medida cero, permitiendo calcular el área bajo su curva de manera precisa.
teorema fundamental del cálculo

El teorema fundamental del cálculo, en el contexto de Riemann, establece la conexión entre la derivación y la integración. Afirma que la integral de una función continua en un intervalo puede calcularse usando una antiderivada. Esto unifica el cálculo diferencial e integral, facilitando el análisis matemático.
https://www.youtube.com/watch?v=Ec-cGjh0Fr0
continuidad

En el contexto de Riemann, la continuidad se refiere a funciones que no presentan saltos o discontinuidades en su dominio. Riemann estudió estas funciones para desarrollar su teoría de integración, permitiendo calcular áreas bajo curvas incluso cuando las funciones no son perfectamente suaves, ampliando así el análisis matemático.
https://www.youtube.com/watch?v=sD0NjbwqlYw
límite

En el contexto de Riemann, el límite se refiere al proceso de aproximación de la suma de áreas bajo una curva mediante particiones cada vez más finas. Esto es fundamental para definir la integral de Riemann, donde el límite de estas sumas de Riemann converge a la integral exacta de una función.
https://www.youtube.com/watch?v=CXCtqBlEZ7g
función
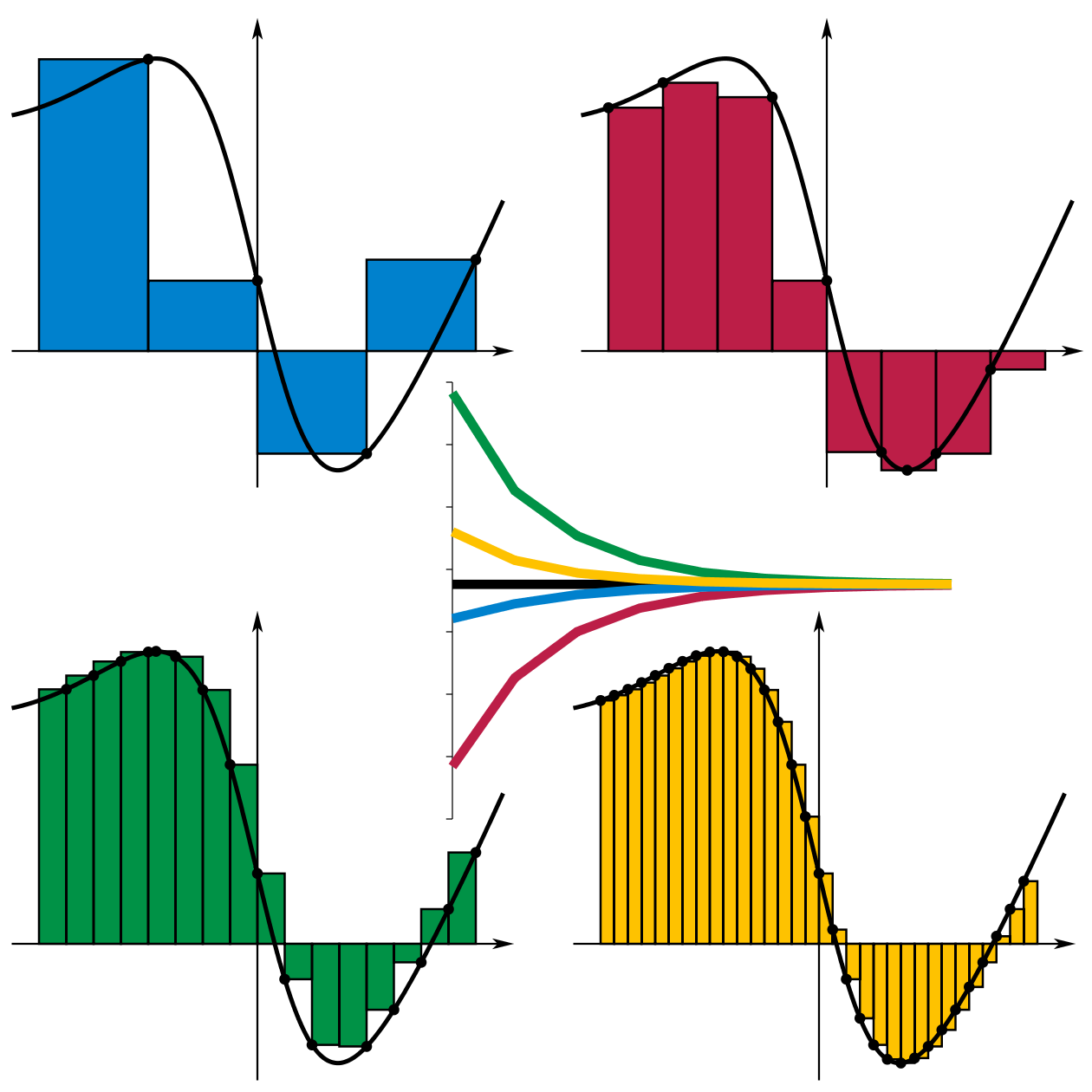
En el contexto de Riemann, una función se refiere a una relación matemática que asigna valores a cada punto de un dominio. En el análisis de Riemann, las funciones son fundamentales para definir integrales, permitiendo calcular áreas bajo curvas y entender el comportamiento de funciones complejas.
intervalo
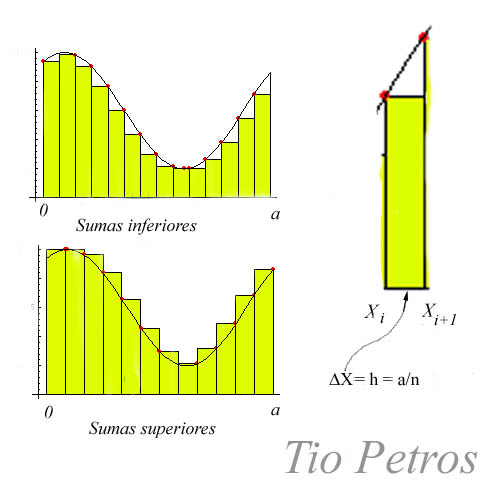
En el contexto de Riemann, un intervalo se refiere al rango de valores en el que se evalúa una función para calcular una integral. Los intervalos se dividen en subintervalos, y se utilizan sumas de Riemann para aproximar el área bajo la curva de la función en ese intervalo.
suma de riemann
La suma de Riemann es un método para aproximar el valor de una integral definida. Consiste en dividir el intervalo de integración en subintervalos, calcular el valor de la función en puntos específicos de estos subintervalos y sumar los productos de estos valores por la longitud de los subintervalos.
https://www.youtube.com/watch?v=YTKQswb60Pw
Lebesgue

El matemático Henri Lebesgue, conocido por su integral, tenía un interés peculiar: le fascinaba coleccionar relojes antiguos. Esta afición reflejaba su amor por la precisión, tanto en el tiempo como en las matemáticas.
https://www.youtube.com/watch?v=gHUZFXvy4yE
medida de lebesgue

La medida de Lebesgue es una herramienta fundamental en la teoría de la medida, que permite asignar un "tamaño" a conjuntos más generales que los intervalos. Desarrollada por Henri Lebesgue, es esencial para la integración de funciones más complejas, extendiendo la integral de Riemann y facilitando el análisis matemático moderno.
https://www.youtube.com/watch?v=kWXf-4S_VeY
integral de lebesgue

https://www.youtube.com/watch?v=LDNDTOVnKJk
El integral de Lebesgue es una herramienta matemática que extiende el concepto de integral, permitiendo integrar funciones más generales que las permitidas por la integral de Riemann. En el contexto de la teoría de Lebesgue, se centra en medir conjuntos y funciones, proporcionando mayor flexibilidad y precisión en el análisis.
función medible
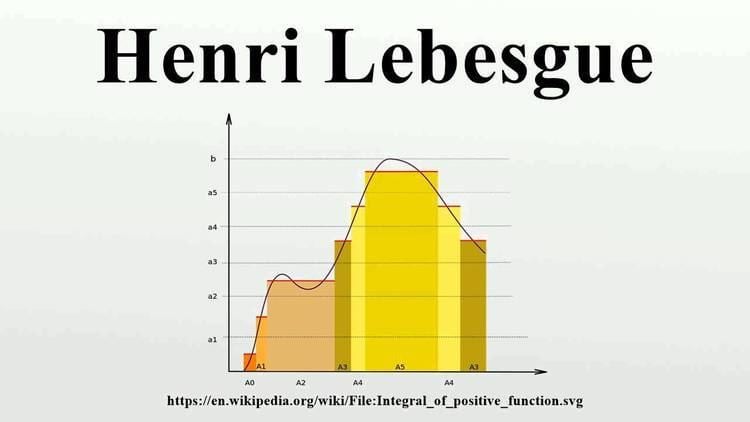
https://www.youtube.com/watch?v=lwPNXrUXEhA
Una función medible en el contexto de la teoría de Lebesgue es aquella que preserva la estructura de la medida. Es decir, para cualquier conjunto medible, la imagen inversa bajo la función también es medible. Esto es crucial para integrar funciones en el sentido de Lebesgue.
convergencia dominada
https://www.youtube.com/watch?v=KfEHmwZLNGc
La convergencia dominada es un teorema fundamental en la teoría de la medida de Lebesgue. Establece que si una sucesión de funciones medibles está dominada por una función integrable, y converge puntualmente, entonces su integral también converge al límite de las integrales de las funciones.
espacio lp

Espacio \( L^p \) es un concepto fundamental en análisis funcional y teoría de la medida, relacionado con la integral de Lebesgue. Estos espacios consisten en funciones cuya \( p \)-ésima potencia es integrable. Son cruciales para estudiar convergencia, continuidad y dualidad en contextos matemáticos avanzados.
https://www.youtube.com/watch?v=nDtw1l6WtQ4
convergencia monótona

https://www.youtube.com/watch?v=mWhJfEGdPGc
La convergencia monótona, en el contexto de la integral de Lebesgue, se refiere al teorema de convergencia monótona. Este establece que si una sucesión de funciones medibles no negativas converge puntualmente de manera monótona a una función límite, entonces la integral de la sucesión converge a la integral de la función límite.
teorema de tonelli

https://www.youtube.com/watch?v=l3FcK-Lx0oA
El teorema de Tonelli, en el contexto de la integral de Lebesgue, establece que si una función es no negativa y medible en el producto de dos espacios medibles σ-finitos, entonces se puede integrar iteradamente. Esto permite calcular integrales dobles como iteración de integrales simples.
teorema de fubini

https://www.youtube.com/watch?v=clgyuPrpLPs
El teorema de Fubini, en el contexto de la integral de Lebesgue, permite intercambiar el orden de integración en integrales dobles. Esto es crucial para calcular integrales en espacios producto, siempre que las funciones sean integrables y las medidas sean σ-finitas, garantizando resultados consistentes y precisos.
AI Report
Essay
**Título: La Contribución de Henri Léon Lebesgue a la Teoría de la Medida**
Henri Léon Lebesgue, un matemático francés nacido en 1875, es ampliamente reconocido por su desarrollo de la teoría de la medida, la cual ha tenido un impacto profundo en el análisis matemático y en la teoría de la integración. Su obra más notable, "Intégrale, longueur, aire" publicada en 1902, sentó las bases para el concepto moderno de medida y ha sido fundamental en la evolución de la integración, superando las limitaciones del cálculo de integrales de Riemann (Lébesgue, 1902). Este ensayo explorará las innovaciones de Lebesgue en la medida, su impacto en el análisis matemático y su legado en la educación matemática.
La teoría de la medida de Lebesgue se basa en la idea de que es posible medir conjuntos de manera más general que lo que permitía la teoría de Riemann. Mientras que la integral de Riemann está limitada a funciones continuas y a intervalos en la recta real, la integral de Lebesgue extiende esta idea a un conjunto más amplio de funciones y espacios. Lebesgue introdujo el concepto de "medida" como una forma de asignar un valor numérico a conjuntos, lo que permite la integración de funciones más complicadas, incluyendo aquellas que presentan discontinuidades (Halmos, 1974). Esta generalización es crucial, ya que muchas funciones en análisis matemático no son integrables en el sentido de Riemann, pero sí lo son en el sentido de Lebesgue.
El impacto de la teoría de la medida de Lebesgue en el análisis matemático es innegable. Su enfoque ha permitido a los matemáticos abordar problemas más complejos en diversas áreas, incluyendo la teoría de la probabilidad, la estadística y la teoría funcional. La integral de Lebesgue no solo es más flexible, sino que también se adapta mejor a las necesidades de los matemáticos que trabajan con funciones en espacios de dimensión infinita (Rudin, 1976). Esto ha llevado a un desarrollo más robusto de la teoría de la probabilidad, donde la noción de medida juega un papel crucial en la definición de probabilidades.
Además, el legado de Lebesgue se extiende a la educación matemática, donde su enfoque ha influido en la forma en que se enseña la integración y la teoría de la medida. Los cursos de análisis matemático modernos a menudo incluyen la teoría de Lebesgue como parte fundamental del currículo, lo que refleja su relevancia continua en el campo. La claridad y la profundidad de su trabajo han proporcionado a los estudiantes y a los educadores una base sólida sobre la cual construir un entendimiento más avanzado de las matemáticas (Stein & Shakarchi, 2005).
En conclusión, Henri Léon Lebesgue ha dejado una huella indeleble en el mundo de las matemáticas a través de su desarrollo de la teoría de la medida. Su enfoque innovador ha permitido la integración de un amplio espectro de funciones y ha transformado el campo del análisis matemático. El impacto de su trabajo sigue siendo evidente en la educación matemática y en la investigación contemporánea, asegurando que su legado perdure en el tiempo. A medida que las matemáticas continúan evolucionando, la obra de Lebesgue seguirá siendo un pilar fundamental en la comprensión de la medida y la integración.
**Referencias**
Halmos, P. R. (1974). *Finite-dimensional vector spaces*. Springer.
Lébesgue, H. (1902). *Intégrale, longueur, aire*. Gauthier-Villars.
Rudin, W. (1976). *Principles of mathematical analysis*. McGraw-Hill.
Stein, E. M., & Shakarchi, R. (2005). *Real analysis: Measure theory, integration, and Hilbert spaces*. Princeton University Press.
Lesson Plan
### Plan de Lección: Introducción a los Lebesgue y su Mantenimiento
**Curso:** Técnicas de Mantenimiento de Equipos
**Duración:** 2 horas
**Objetivos de Aprendizaje:**
- Comprender qué es un Lebesgue y su función en sistemas técnicos.
- Identificar los componentes de un Lebesgue.
- Aprender sobre los procedimientos de mantenimiento de Lebesgue.
---
#### Materiales Necesarios:
- Proyector y pantalla
- Presentación en PowerPoint sobre Lebesgue
- Documentación técnica sobre Lebesgue
- Ejemplos de Lebesgue (físicos o imágenes)
- Herramientas básicas de mantenimiento
- Cuestionarios para evaluación
---
### Estructura de la Clase:
#### 1. **Introducción (15 minutos)**
- **Saludo y presentación del tema.**
- Pregunta inicial: "¿Qué saben sobre el concepto de Lebesgue?"
- Breve introducción a la historia y la importancia del Lebesgue en la industria.
#### 2. **Conceptos Teóricos (30 minutos)**
- **Definición de Lebesgue:**
- Explicar qué es un Lebesgue y su función en sistemas como la medición de espacios, análisis matemático, etc.
- **Componentes de un Lebesgue:**
- Desglosar los componentes principales de un Lebesgue y su funcionamiento.
- Uso de imágenes o diagramas en la presentación para ilustrar cada componente.
#### 3. **Aplicaciones Prácticas (20 minutos)**
- **Ejemplos de uso de Lebesgue:**
- Presentar diferentes aplicaciones en la industria.
- Discusión sobre cómo se utilizan en la práctica y su impacto en la eficiencia de los sistemas.
#### 4. **Mantenimiento de Lebesgue (30 minutos)**
- **Procedimientos de Mantenimiento:**
- Explicar los pasos necesarios para el mantenimiento de un Lebesgue.
- Discutir la importancia del mantenimiento regular y las consecuencias de la falta de este.
- **Demostración Práctica:**
- Si es posible, realizar una demostración en vivo sobre cómo realizar una tarea de mantenimiento básica en un Lebesgue.
#### 5. **Evaluación y Cierre (25 minutos)**
- **Cuestionario:**
- Entregar un cuestionario para evaluar la comprensión de los estudiantes sobre el tema.
- **Discusión abierta:**
- Permitir que los estudiantes hagan preguntas y compartan sus experiencias relacionadas con el tema.
- **Conclusión:**
- Resumir los puntos clave aprendidos durante la clase.
---
### Actividades y Tareas:
- **Tarea para el hogar:** Investigar un tipo específico de Lebesgue utilizado en su campo de estudio y preparar una breve presentación para la próxima clase.
- **Refuerzo:** Pueden formar grupos para discutir los diferentes tipos de Lebesgue y su mantenimiento en el entorno laboral.
---
### Evaluación:
- Evaluar la comprensión mediante el cuestionario y la participación en la discusión.
- Revisar las presentaciones de la tarea para evaluar la investigación y la comprensión del tema.
---
Este plan de lección está diseñado para ser interactivo y práctico, permitiendo a los estudiantes no solo aprender sobre Lebesgue, sino también aplicar su conocimiento en situaciones reales.
Class Syllabus Outline
### Sílabo del Curso: Introducción a la Teoría de Lebesgue
**Descripción del Curso:**
Este curso ofrece una introducción a la teoría de la medida y la integral de Lebesgue. Se explorarán conceptos fundamentales y se desarrollarán las herramientas necesarias para entender la importancia de la medida en el análisis matemático moderno.
**Objetivos del Curso:**
- Comprender los principios básicos de la teoría de la medida.
- Aprender a construir la medida de Lebesgue y su relación con la medida de Borel.
- Desarrollar habilidades para calcular la integral de Lebesgue y compararla con la integral de Riemann.
- Aplicar la teoría de Lebesgue a problemas en análisis real y teoría de la probabilidad.
**Requisitos Previos:**
- Conocimientos básicos de análisis matemático, incluyendo límites, continuidad y funciones.
- Familiaridad con la integral de Riemann.
---
### Contenido del Curso
**Semana 1: Introducción a la Medida**
- Definición de medida.
- Propiedades de las medidas.
- Ejemplos de medidas: longitud, área, volumen.
**Semana 2: Conjuntos Medibles**
- Conjuntos de Borel.
- Propiedades de los conjuntos medibles.
- Teorema de la σ-aditividad.
**Semana 3: Construcción de la Medida de Lebesgue**
- Medida de Lebesgue en la recta real.
- Construcción a partir de intervalos.
- Propiedades de la medida de Lebesgue.
**Semana 4: Funciones Medibles**
- Definición de función medible.
- Propiedades de las funciones medibles.
- Ejemplos de funciones medibles y no medibles.
**Semana 5: Integral de Lebesgue**
- Definición de la integral de Lebesgue.
- Comparación con la integral de Riemann.
- Teorema de convergencia de Lebesgue.
**Semana 6: Teoremas Fundamentales**
- Teorema de la convergencia monótona.
- Teorema de la convergencia dominada.
- Propiedades de la integral de Lebesgue.
**Semana 7: Aplicaciones de la Integral de Lebesgue**
- Aplicaciones en análisis funcional.
- Aplicaciones en teoría de la probabilidad.
- Ejemplos prácticos.
**Semana 8: Medidas en Espacios Métricos**
- Extensión de la medida de Lebesgue a espacios más generales.
- Introducción a la teoría de medidas en espacios métricos.
- Ejemplos de medidas más generales.
**Semana 9: Medidas y Probabilidad**
- Relación entre medidas y probabilidad.
- Espacios de probabilidad y medidas de probabilidad.
- Teoremas de probabilidad en el contexto de la medida de Lebesgue.
**Semana 10: Repaso y Proyecto Final**
- Repaso de los conceptos clave.
- Presentación de proyectos finales.
- Discusión sobre aplicaciones futuras en investigación.
---
### Evaluación
- **Tareas (30%)**: Ejercicios semanales basados en los temas tratados.
- **Exámenes (40%)**: Dos exámenes parciales que evalúan el entendimiento de los conceptos clave.
- **Proyecto Final (30%)**: Un proyecto que explora un tema relacionado con la teoría de Lebesgue, presentado al final del curso.
### Bibliografía
- Halmos, P. R. (1974). "Measure Theory". Springer-Verlag.
- Rudin, W. (1987). "Real and Complex Analysis". McGraw-Hill.
- Folland, G. B. (1999). "Real Analysis: Modern Techniques and Their Applications". Wiley.
---
**Notas Adicionales:**
- Las clases incluirán discusiones, ejercicios prácticos y sesiones de preguntas y respuestas.
- Se fomentará la participación activa de los estudiantes a través de debates y presentación de ejemplos.
- Todos los materiales del curso estarán disponibles en línea a través de la plataforma del curso.
Learning Objectives
Claro, aquí tienes algunos objetivos de aprendizaje en español (es-ES) para un curso sobre la integral de Lebesgue dirigido a estudiantes de formación profesional técnica:
### Objetivos de Aprendizaje
1. **Comprender los Fundamentos de la Teoría de la Medida:**
- Explicar el concepto de medida y su importancia en el análisis matemático.
- Distinguir entre diferentes tipos de medidas, como la medida de Lebesgue y la medida de Borel.
2. **Desarrollar Habilidades en la Integral de Lebesgue:**
- Calcular la integral de Lebesgue de funciones simples y funciones adaptadas.
- Comparar la integral de Lebesgue con la integral de Riemann y entender sus diferencias y aplicaciones.
3. **Aplicar Propiedades de la Integral de Lebesgue:**
- Utilizar propiedades como la linealidad, la monotonía y el teorema de convergencia para resolver problemas prácticos.
- Aplicar el teorema de Dominio Monótono y el teorema de Convergencia Dominada en ejemplos concretos.
4. **Resolver Problemas de Aplicación Práctica:**
- Analizar problemas de la vida real que puedan resolverse mediante la integral de Lebesgue, como en física y estadísticas.
- Desarrollar la capacidad para modelar situaciones complejas utilizando la teoría de la medida y la integral de Lebesgue.
5. **Fomentar el Pensamiento Crítico y la Resolución de Problemas:**
- Evaluar y criticar diferentes enfoques para la integración de funciones en contextos técnicos.
- Fomentar la habilidad para formular preguntas y buscar soluciones a problemas matemáticos complejos.
6. **Conocer las Aplicaciones de la Integral de Lebesgue en la Tecnología:**
- Identificar cómo la integral de Lebesgue se utiliza en campos como la informática, la ingeniería y la economía.
- Explorar ejemplos de cómo la teoría de la medida influye en algoritmos y técnicas de análisis de datos.
Estos objetivos buscan proporcionar a los estudiantes una base sólida en la teoría de Lebesgue, así como habilidades prácticas que les sean útiles en su futura carrera técnica.
Quiz Questions
Claro, aquí tienes cinco preguntas de opción múltiple sobre Henri Léon Lebesgue y su trabajo en matemáticas:
### Pregunta 1:
¿En qué área de las matemáticas es más conocido Henri Lebesgue?
A) Álgebra
B) Geometría
C) Análisis matemático
D) Teoría de números
**Respuesta:** C) Análisis matemático
---
### Pregunta 2:
¿Qué concepto fundamental introdujo Lebesgue en su trabajo sobre la integración?
A) Integral de Riemann
B) Integral de Lebesgue
C) Integral de Stieltjes
D) Integral de Fourier
**Respuesta:** B) Integral de Lebesgue
---
### Pregunta 3:
¿Cuál es el objetivo principal de la teoría de la medida de Lebesgue?
A) Calcular áreas de figuras geométricas
B) Proporcionar una forma de medir conjuntos en espacios más generales
C) Resolver ecuaciones diferenciales
D) Establecer propiedades de funciones continuas
**Respuesta:** B) Proporcionar una forma de medir conjuntos en espacios más generales
---
### Pregunta 4:
¿En qué año publicó Lebesgue su obra más influyente, "Leçons sur l'intégration et la recherche des fonctions primitives"?
A) 1902
B) 1904
C) 1906
D) 1910
**Respuesta:** B) 1904
---
### Pregunta 5:
¿Qué propiedad importante tiene la integral de Lebesgue en comparación con la de Riemann?
A) Es más fácil de calcular
B) Puede integrar funciones discontinuas
C) Siempre da un resultado más grande
D) Solo se aplica a funciones continuas
**Respuesta:** B) Puede integrar funciones discontinuas
---
Espero que estas preguntas te sean útiles. ¡Si necesitas más información o preguntas adicionales, no dudes en pedirlo!